Izradio: Dane

Objašnjenje problema, kako znati je li točka unutar mnogokuta

 

Mnogokut se izradi tako da mišem pikamo točku po točku, te tako stvorimo niz koordinata(x i y) točaka od n članova. Zatim, nakon što iscrtamo mnogokut piknemo točku za koju želimo provjeriti je li ili nije u mnogokutu.

 

Postupak provjere je ovakav:

Povučemo polupravac od provjeravane točke usporedno s x-osi u njenom pozitivnom smjeru (teoretski je moguće povuči polupravac u bilo kojem smjeru, ali radi jednostavnosti izabrao sam ovakao). Nakon toga treba izbrojiti presijecišta polupravca sa stranicama mnogokuta. Ako se dogodi da polupravac prolazi točno kroz neki vrh od mnogokuta, tada se čini slijedeće. Ukoliko je taj vrh mjesno najveća ili najmanja vrijednost (y[i]>y[i-1] & y[i]>y[i+1] ili y[i]<y[i-1] & y[i]<y[i+1]) tada to zanemarimo, ukoliko nije to (y[i-1]<y[i]<y[i+1]) tada to gledamo kao da sječe stranicu mnogokuta, znači gledamo kao sijecište. Ukoliko je broj sijecišta neparan broj, tada je provjeravana točka unutar mnogokuta, ako je paran broj tada je točka izvan mnogokuta (Vidi sliku 1).

 

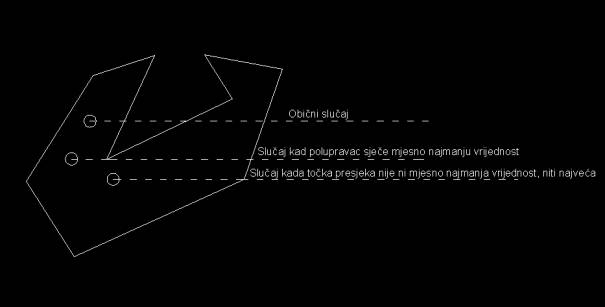
Slika 1

 

Objašnjenje programa u javi

 

1)     U kućicu ubacim broj koji određuje broj vrhova u mnogokutu.

2)     Pomoću slušača ActionListener-a (actionPerformed), ta vrijednost se izvadi koja je u prvi mah string, da bi ga naknadno pretvorio u integer(cijeli broj), ta varijabla je označena kao ‘brcl’.

3)     Nakon toga s klikovima miša, pomoću slušača MouseListener-a koristeći metodu mouseClicked, dobivam podatke o koordinatama gdje sam kliknuo. Svaku primljenu koordinatu pospremam u niz, odvojeno za x i y (x[i], y[i]).

public void mouseClicked(MouseEvent e) {

if (br<brcl) {

x[br]=e.getX();

y[br]=e.getY(); }

br=br+1;

if (br>brcl) { xt=e.getX(); yt=e.getY(); }

repaint();

}

 

4)     Nakon svakog primanja koordinata, odmah se poziva paint metoda koja odmah iscrta do tada kliknute točke i stranice. Evo izvadka iz paint metode:

if (br<=brcl) {

for (int i=0; i<br; i++) {

if (i>0) { Line2D.Double crta3 =new Line2D.Double(x[i-1], y[i-1], x[i], y[i]); g2.draw(crta3); } /*Crta crte u skladu s pikanjem točaka*/

Shape krug1=new Ellipse2D.Double (x[i]-r1, y[i]-r1, 2*r1, 2*r1);

g2.draw(krug1); } } /*Iscrtavaju se točke mnogokuta nakon klika mišem*/

 

5)     Nakon što se sve točke unesu mišem, nakon toga kliknem još jednu točku čije koordinate smjestim u xt i yt.

6)     Nakon toga idem istraživati sjecišta pozitivnog polupravaca zadane točke y=yt i pravaca svake stranice mnogokuta y-y[i]=((x[i+1]-x[i])/(y[i+1]-y[i]))*(x-x[i]). Uvjet je li se neko sjecište nalazi na pozitivnom polupravcu i na nekoj stranici je ovakav:

-najprije izračunam x-koordinatu sjecišta xg=(((x[i+1]-x[i])/(y[i+1]-y[i]))*(yt-y[i])+x[i]; koje mora zadovoljiti uvjet xt<xg (ovo je uvjet za polupravac)

-zatim također mora biti zadovoljen uvjet da y-koordinata ispitivane točke bude između y-koordinata točaka na mnogokutu koje čine pojedinu stranicu

(yt<y[i] i yt>y[i+1]) ili (yt>y[i] i yt<y[i+1]).

-ako je zadovoljen taj uvjet onda povečam brojač presjecišta ‘brs’ za jedan

Napomena: za zadnju stranicu moram staviti poseban uvjet, s obzirom da nije jednostavno x[1] i x[brcl-1] jednostavno uklopiti u for-petlju

-nakon toga gledam koliki je ostatak kad podijelim brs/2, te ako je ostaka nula, tada je točka izvan mnogokuta, a ako je različito od toga onda je unutar.

if (brs%2==0) { g2.drawString("Točka je izvan mnogokuta",100,100); }

if (brs%2!=0) { g2.drawString("Točka je unutar mnogokuta",100,100); }

 

7)      Također sličnu stvar napravim i za pojedine točke, jer se može dogoditi da pravac taman prolazi kroz neku točku mnogokuta, a ne stranicu. Tu me zanima je li y od neke točke ima mjesnu krajnost. Ako ima tada ju ne brojim, tj. ništa ne pridodam brs, a ako nije onda brs=brs+1, tj. tada na točku gledam kao na presjecište sa stranicom.